"Le forme create dal matematico, come quelle create dal pittore o dal poeta, devono essere belle; le idee, come i colori o le parole, devono legarsi armoniosamente. La bellezza è il requisito fondamentale: al mondo non c'è un posto perenne per la matematica brutta."
Ecco di cosa parla il libro: del fascino della matematica, intesa come disciplina che deve soddisfare criteri estetici, creativi ed artistici. La matematica come arte, in quanto richiede creatività, deve generare prodotti necessariamente belli e trasmettere messaggi, ovviamente a chi è in grado di coglierli (qualcuno sarà svenuto dopo questa affermazione.... I saliii portate i saliiii).
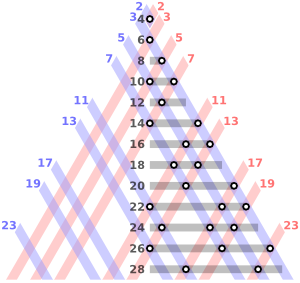
Il romanzo racconta la vita di Petros, un fallito secondo i suoi famigliari, che dedica la propria vita alla matematica, con un amore per essa che diventa ossessione e che lo porta alla distruzione fisica e psicologica, perché perso nella ricerca della dimostrazione della cosiddetta "Congettura di Goldbach". La congettura, secondo la quale ogni numero pari maggiore di due sarebbe la somma di due numeri primi, fu formulata per la prima volta dal matematico russo Goldbach, ma mai dimostrata da nessuno. La dimostrazione della congettura è uno dei tre maggiori problemi irrisolti della matematica e circola nientepopodimeno che dall'epoca di Eulero e Leibniz.
I numeri primi sono quei numeri che possono essere divisi solo per sé stessi e per uno, definiti da qualcuno "gli atomi della matematica". La loro successione sembra caotica e casuale, ma se osservata con maggiore attenzione diventa quasi "magica e misteriosa".
Ma perché Petros vuole risolvere la congettura, compromettendo la sua vita personale, rinunciando all'amore e ad una vita di relazione? Semplice. Per diventare immortale, per poter essere ricordato nel tempo. Per un matematico la mediocrità non serve a nulla, bisogna essere esageratamente bravi. Per esempio, risolvere per primi un problema importante, anzi no, importantissimo; come la dimostrazione della congettura.
"Archimede sarà ricordato quando Eschilo sarà dimenticato, perché le lingue muoiono ma le idee matematiche no. Immortalità è forse una parola ingenua ma, qualunque cosa significhi, un matematico ha le migliori probabilità di conseguirla."
Petros dedica vent’anni al tentativo di risoluzione della congettura. In questo periodo non fa altro che studiarla e sognarla, ossessionato dal tempo che passa, perché la mente di un matematico è fertile e produttiva solo quando è in giovane età.
"Nessun matematico può permettersi di dimenticare che la matematica, più di qualsiasi altra arte o di qualsiasi altra scienza, è un'attività per giovani" diceva Harold Hardy.
Lui crede fermamente nel fatto che se la congettura è vera, allora esiste una dimostrazione disponibile al primo che la trova. si ispira cioè a ciò che diceva il grande matematico David Hilbert nel 1900: "Noi dobbiamo sapere, noi sapremo".
Ma ad un certo punto.... arriva un ometto strano, ipocondriaco, magrissimo, con gli occhiali, un austriaco chiamato Godel. Che gli fa crollare il mondo addosso, perché dimostra..... che non è detto che debba esistere una dimostrazione, ossia che la congettura potrebbe essere anche indimostrabile. La vita di Petros improvvisamente perde di senso. E... si arrende.
Molto interessante il romanzo, che mescola personaggi inventati (Petros) con persone famose realmente esistite, quali Hardy, Littlewood, Ramanujan, Godel e Turing e che riesce ad appassionare anche chi non sa nulla di matematica. Il libro porta a chiedersi cosa sia la matematica e perché l'uomo ne sia così affascinato. E ci fa capire che l'uomo non deve limitarsi a cercare di raggiungere solo obiettivi raggiungibili, ma deve osare. Solo così è possibile il progresso; senza lo sforzo immane di persone che spendono la propria vita dietro obiettivi sulla carta impossibili, la maggior parte delle scoperte scientifiche non ci sarebbero state.