Δx Δp ≥ ½ ħ ’s Comments (group member since Apr 24, 2011)

Δx Δp ≥ ½ ħ ’s comments from the Homework Study Helpers! =P group.

y - y1 = m (x - x1)

y-(-3)=(8/7)(x-5)

y+3=(8/7)(x-5)

7y+21=8x-40

21+40=8x-7y

8x-7y=61

Google Form?

survey monkey?

6*9*x = 10x - 2
54x = 10x - 2
44x = -2
x = -2/44 = -1/22

are you sure that the problem was correct?

hehe.. sorry.. i've just had holiday :P

well, i think your answer for the last is correct

in other way,

7n+2[2(1-n)-2(1+n)]=14
7n + 2 [ 2 {(1-n) - (1+n)} ] = 14
7n + 4 [ 1-n - 1-n] = 14
7n + 4 [-2n] = 14
7n - 8n = 14
-n = 14
n = -14

4. yes
5. yay
9. yep
10. yuhu
11. right
12. correct
16. true
20. great

15. yes, you did

16. 15+5[5+3(2+2)] = 15+5[5+3(4)] = 15 + 5[5+12] = 15 + 5[17] = 15 + 85 = 100
7 - 45/[5+2(6/3)] = 7-45/[5+4] = 7 - 45/9 = 7 - 5 = 2

so, 100/2 = 50

^ both of them i think

which is part?

1. because of the Exterior Angle Inequality Theorem. (ask to google)

2. because if one side of a triangle is bigger than another side, then the first sides opposite angle is also larger than the second sides opposite angle.

3. the largest is for sure, draw the lines on a piece of paper. shows you pretty well what one is the largest. the opposing angle of the largest side, if I'm not mistaken

you're welcome :)

@Abby: here we go...



look up for step by step. if you find it hard to understand, ask me, which part is :)

Rh = Rhesus

http://en.wikipedia.org/wiki/Rhesus_f...

Grant wrote: "what do we do 2 win the contest?!?!? whats the prize???"

yes... the prize...

ah, i'm forgetting the important one,

Area is measured in "square" units.

For example, Area of a square = side times side. Since each side of a square is the same, it can simply be the length of one side squared. If a square has one side of 4 inches, the area would be 4 inches times 4 inches, or 16 square inches. (Square inches can also be written in².)

Be sure to use the same units for all measurements. You cannot multiply feet times inches, it doesn't make a square measurement. You have to convert the different unit one to other units.

Sky**Rainbow Rose** wrote: "How do you find the missing measurement of these triangles?

Examples:

Area = 100 yd squared Base = 25 yd squared Height = ?

Area = 1,955 cm squared Height = 85 cm Base = ?"
____________________________________________________

Okay, the formula for area of a triangle given by

A = ½ x b x h


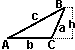
A = area
b = base
h = height

or, area of the triangle equals one half times the base times the height. so, from the exercises:

1)
A = 100 yd²
b = 25 yd
h?
re-arrange the formula for area of a triangle:

A = ½ x b x h ... multiple both sides by 2
2A = b x h ...... divide both sides by "b"
2A/b = h

so, we get the formula to find the height
h = 2A/b
plug in the numbers
h = 2 (100) /25 = 200/25 = 8

thus, the height of the triangle is 8 yard (the unit is must be equal to others)

2)
A = 1,955 cm²
h = 85 cm
so,

A = ½ x b x h ... multiple both sides by 2
2A = b x h ...... divide both sides by "h"
2A/h = b

so,
b = 2A/h , plug in the numbers
b = 2 (1,955) / 85 = 3910/85 = 46

the base of the triangle is 46 cm

^ errr. is it a formula for volume of a cube? not formula for surface area of a cube?

to get 3rd answer, you must see the point B (-2,-4), C (6, -4)

the general form of a line equation is

y = ax +b

plug in point B to the general equation:
(-4) = a (-2) + b
-4 = -2a + b ...................... (1)

plug in point C to the general equation
(-4) = a (6) + b
- 4 = 6a + b ...................... (2)

so, we have two equations for (1) and (2)

- 4 = -2a + b = 6a + b
-2a + b = 6a + b
-2a = 6a

the only possibility that comply this equation, "a" must be zero.
-2 (0) = 6(0) = 0

so, we get a = 0

subtitute "a" to (1) equation
-4 = -2a + b
-4 = -2(0) + b
b = -4

in other way, you can find it by subtitute "a" to 2nd equation
-4 = 6(a) + b
-4 = 6(0) + b
b = -4

you get a and b, so, plug them to the general equation

y = ax + b
y = (0)x + (-4)
y = 0 -4
y = -4

proven!

actually, the first and the second answer are similiar. but in 2nd, we don't have m or slope. so, to get m, we use a formule to find it.

The slope m of the line through the
points (x1, y1) and (x2, y2) is given by


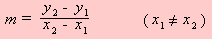
so, from the points A(1, 5), B(-2, -4), we must label the points as x1, y1, x2, y2. Label the points as x1 = 1, y1 = 5, x2 = -2, and y2 = -4.
To find the slope m of the line segment joining the points, use the slope formula

m = [(-4)- 5]/[(-2)-1)] = -9/-3 = 3

or, you can label point A as (x2,y2) and B as (x1, y1)
x1 = -2, y1 = -4, x2 = 1, y2 = 5
so,
m = [5 - (-4)]/[1 - (-2)] = 9/3 = 3


After you got "m", you use formula in first answer.
y - y1 = m (x - x1)
m is the calculated slope, and (x1, y1) are the coordinates of the given point (you can use point A or point B, it gives same result as showed in 2nd answer)

which part is don't u get?

1. Use the point-slope form of the equation of a line:

y - y1 = m (x - x1)

m is the given slope, and (x1, y1) are the coordinates of the given point.

Then solve the result for y to put it into slope-intercept form.

m = -1 ; (x1,y1) = (6,-4)

so
y - y1 = m (x-x1)
y - (-4) = -1 (x - 6)
y + 4 = -x + 6
y = -x - 4


2. Point-Slope Form: y - y1 = m(x - x1)
x1: x coordinate of a point they give you [doesn't matter which point]
y1: y coordinate of a point they give you [has to be the coordinate that came with x1]
m: slope

You could do point-slope form directly, but you don't have slope

Slope: (y2 - y1)/(x2 - x1) [It doesn't matter which point you choose to by y1 or y2, as long as y1 corresponds to x1 and y2 corresponds to x2 ]

(5-(-4))/(1-(-2))= 9/3= 3

Choose a point [either A or B] and plug everything in:
Using point A: y-5=3(x-1) ---> y = 3x + 2
Using point B: y+4=3(x+2) ---> y = 3x + 2

3. it's simple
y = -4

There is no change in the Y-coordinates, therefore Y will always equal the same thing, regardless of X, in this case, negative four.