Odd Job

A problem by Russian mathematician Viktor Prasolov:

On a piece of graph paper, is it possible to paint 25 cells so that each of them has an odd number of painted neighbors? (“Neighboring” cells have a common side.)

Let nk be the number of painted cells with exactly k painted neighbors, and let N be the number of common sides of painted cells. Each common side belongs to exactly two painted cells, so

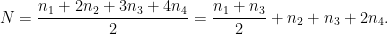
$\displaystyle N = \frac{n_{1} + 2n_{2} + 3n_{3} + 4n_{4}}{2} = \frac{n_{1} + n_{3}}{2} + n_{2} + n_{3} + 2n_{4}.$